Сумма внутренних углов многоугольника является важной характеристикой в геометрии, которая зависит от количества сторон фигуры. Рассмотрим основные формулы и закономерности для расчета этой величины.
Содержание
Сумма внутренних углов многоугольника является важной характеристикой в геометрии, которая зависит от количества сторон фигуры. Рассмотрим основные формулы и закономерности для расчета этой величины.
Основная формула суммы углов
Для выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
| Формула | S = (n - 2) × 180° |
| Где | n - количество сторон (углов) многоугольника |
Примеры расчетов для различных многоугольников
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
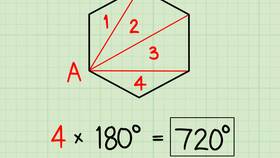
| Шестиугольник | 6 | (6-2)×180° = 720° |
Дополнительные свойства
Для правильных многоугольников
В правильном многоугольнике все углы равны, поэтому каждый внутренний угол (α) можно найти по формуле:
- α = [(n - 2) × 180°] / n
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника всегда равна 360°, независимо от количества сторон:
- Σ внешних углов = 360°
Практическое применение
Знание суммы углов многоугольника позволяет:
- Определять тип геометрической фигуры
- Решать задачи на построение
- Проверять корректность чертежей
- Вычислять неизвестные углы в многоугольниках
Пример задачи
В пятиугольнике четыре угла равны 110°, 90°, 130° и 120°. Найдите величину пятого угла.
- Сумма углов пятиугольника: (5-2)×180° = 540°
- Сумма известных углов: 110° + 90° + 130° + 120° = 450°
- Неизвестный угол: 540° - 450° = 90°
Формула суммы углов многоугольника является фундаментальным знанием в геометрии, которое находит применение как в теоретических исследованиях, так и в практических расчетах.
